leecode-48-旋转图象

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

题目

思路

可以将整体旋转，解构为按层来旋转。并且，n*n 矩阵最多有 n/2 层。
我们可以从最外层开始，遍历所有层， 每一层都从上边(可以任意选择)开始旋转。
上边从最左边的点开始，依次绕圈找到该坐标旋转后的位置，将其放入，重复四次即可。（因为有四条边）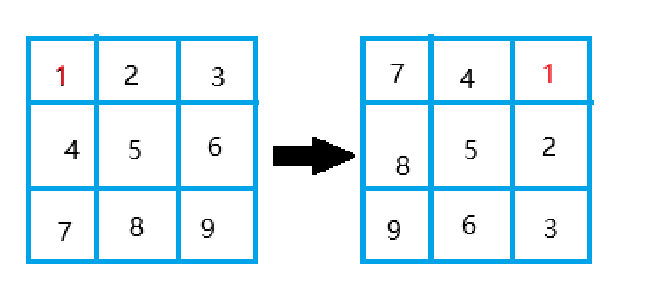

图上就是一个3*3的矩阵旋转变化。在此矩阵中，层数为: n/3 = 1.
看这里1的位置，1为最外层(i = 0)的初始元素，设其初始位置为 (x,y),在这里，x y此时都为0（i），变换后的位置为 (n - 1 - i, x)， 这个就是上边旋转到右边后的坐标算法。可以这么来想：

上边的纵坐标是恒定的（即y不会变，是一条横线），而右边的边横坐标是恒定的（x不会变，是一条竖线），所以我们判定该店对应右边的横坐标与该点原本的纵坐标有关系。具体关系的大小，可以观察，当前边所处的层即为右边横坐标与总层数的差值，即可得右边的横坐标公式： n - 1 - i
至于纵坐标，可以观察到随着当前选取的点不断右移，在右边所对应的纵坐标也不断下移，可推论出右边的纵坐标即为当前点的横坐标 x 最后得出坐标公式 (n - 1 - i, x)

然后右边本来的3旋转到了下边，此时的左边变换是: (n - 1 - i, x) -> (n - 1 - x, x - 1 - i)
最后下边变为左边的对应坐标变换: (n - 1 - x, x - 1 - i) -> (i, n - 1 - x)
第四次就会绕回原点： (i, n - 1 - x) -> (x, i)

代码：

public void rotate(int[][] matrix) {
    int n = matrix.length;

    for (int i = 0; i < n / 2; i++) {// 遍历所有层级。 EXAMPLE: 3 × 3 代表着两层，外面一层，里面一层。
        for (int x = i, y = i; x < (n - i - 1); x++) { // 每一层开始， 从（i,i）处当作起点，依次遍历四个边所对应的坐标
            int targetX = (n - i - 1);
            int targetY = x;
            int tmp = matrix[targetY][targetX];
            matrix[targetY][targetX] = matrix[y][x]; // 起点赋值给右边的

            targetX = (n - 1 - x);
            targetY = (n - 1 - i);
            matrix[y][x] = tmp;
            tmp = matrix[targetY][targetX];
            matrix[targetY][targetX] = matrix[y][x];// 右边的值赋值给底边的

            targetX = i;
            targetY = (n - 1 - x);
            matrix[y][x] = tmp;
            tmp = matrix[targetY][targetX];
            matrix[targetY][targetX] = matrix[y][x];// 底边的值赋值给左边的

            matrix[y][x] = tmp; // 最后将左边的值赋值给原点 x,y 
        }
    }
}