lk_72_medium_editor_distance

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

Insert a character
Delete a character
Replace a character

思路:
两个字符串的编辑距离，由A变为B，在dp的过程中，可以试图去想象两个都是较短的字符串来互相转换。
比如:
A: leetcode B: lintcody
现在我们有了两个字符串需要互相转换，但是我们可以想象一下，假设A是个控字符串，那么空字符串要变成B该如何做呢？此时需要做的就是把B中的字符全部附加过来即可，即A(0) -> B(8) 需要8次操作.反之亦然，B(0) -> A(8)也是需要8次操作。这里操作次数相同是因为两个字符串长度相等.
接下来，再次想象，A(1) -> B(8)呢？我们使用瞪眼法观察可以得到直接拼接剩下7个字符即可，但是代码中是没有瞪眼的，所以我们需要使用一个稍微复杂一些的方法。
A(1) -> B(8)这个转换，我们可以尝试将其转换成 A(1) -> B(7),这样，我们就少进行依次转换操作，我们得到的结果可能是 lintcod,结尾少了一个字符，所以我们需要在此基础上再多做一次操作，添加剩下的这个字符,即 A(1) -> B(8) = A(1) -> B(7) + 1
然后，不断的进行这样的动态规划假设，到最后，会变成 A(1) -> B(1)。

我们可以尝试列出矩阵dp[i][j],来表示长度i的字符串A与长度j的字符串B转换所需最少步骤。
我们很容易得出,dp[0][j] = j, dp[i][0] = i;即空串变为另外一个字符串需要操作次数就是另外一个字符串的长度。

其实，这里A(1) -> B(1)我们观察可以知道不需要进行额外的变换，即0次操作，但是这个推导其实是从如下理论来的:
A(1)其实可以视为当前字符串分为两部分，一部分是空字符串，一部分是这一个字符.
同理， B(1)也是。那么该如何进行A(1) -> B(1)的转换呢？
既然字符串有一个空串，并且我们已知空串变为另外字符的操作，那么我们此时就可以选择如下操作:

1. A的空串拼接B的字符，此时A B 均为长度为1的字符串，并且操作数+1
2. B的空串拼接A的字符，结果同上
3. 若A B当前索引处字符相等，那么两个空串无需做额外操作，直接将索引移动到此处即可。即A(0)向后移动A（1）是小写字母 l， B也是。

在此基础上，我们可以尝试A（2） -> B(2)，根据上面的dp方程可以推出:
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]， dp[i - 1][j - 1]) + 1
需要注意，如果我们当前索引位置字符相等，那么就无需额外操作，即：

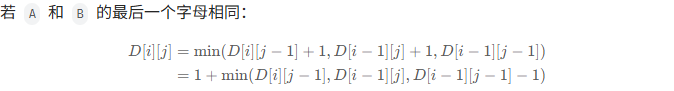
code:

class Solution {
    public int minDistance(String word1, String word2) {
        int n1 = word1.length();
        int n2 = word2.length();

        int[][] dp = new int[n1 + 1][n2 + 1];

        for (int i = 0; i < n1 + 1; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j < n2 + 1; j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i < n1 + 1; i++) {
            for (int j = 1; j < n2 + 1; j++) {
                int m1 = dp[i - 1][j] + 1;
                int m2 = dp[i][j - 1] + 1;
                int m3 = dp[i - 1][j - 1];
                if (word1.charAt(i - 1) != word2.charAt(j - 1)) {
                    m3++;
                }
                dp[i][j] = Math.min(m1, Math.min(m2, m3));
            }
        }
        return dp[n1][n2];
    }
}